RESISTÊNCIA DOS MATERIAIS
Assinale a alternativa que apresenta o valor do torque T que causa uma tensão cisalhante máxima de 75 MPa em um cilindro de aço de diâmetro externo de 25 mm e espessura da parede 2,5 mm, conforme ilustrado abaixo.
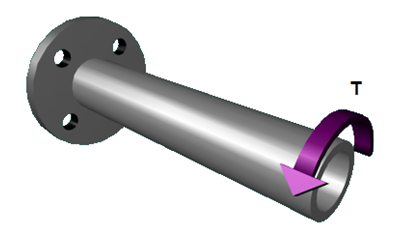
122,98 N.m
243,25 N.m
135,85 N.m
150,34 N.m
170,35 N.m
Uma viga simples AB com um balanço BC suporta um carregamento concentrado P na extremidade do balanço (conforme figura). A extensão principal da viga tem comprimento L e o balanço tem comprimento L/2. Determine a deflexão δC na extremidade do balanço. Use a equação diferencial de terceira ordem da curva de deflexão( a equação da força de cisalhamento). A viga tem rigidez de flexão EI constante.
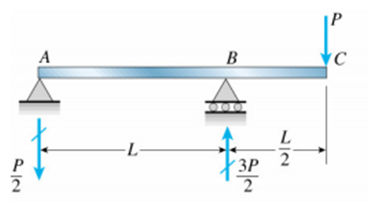
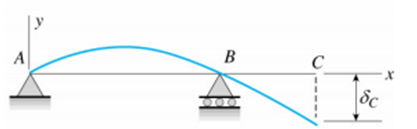
δc = PL³/8EI
δc = PL³/30EI
δc = PL³/24EI
δc = PL²/3EI
δc = PL³/3EI
O eixo de cobre está sujeito às cargas axiais mostradas na figura. Determine o deslocamento da extremidade A em relação à extremidade D se os diâmetros de cada segmento forem dAB = 20 mm, dBC = 25 mm e dCD = 12 mm. Ecobre = 126 GPa.

+ 23,843 mm
+ 10,254 mm
+ 3,8483 mm
– 3,8483 mm
– 1,2543 mm
Qual o valor da deformação especifica normal de uma barra de comprimento inicial 1,75m, que após a aplicação de uma força passa a medir 1,762 m?
0,000506
0,000476
0,00686
0,000214
0,00706
O cabeçote H está acoplado ao cilindro de um compressor por seis parafusos de aço. Se a força de aperto de cada parafuso for 4 kN, determine a deformação normal nos parafusos. Cada um deles tem 5 mm de diâmetro. Se σe=280 Mpa e Eaço=200 GPa, qual é a deformação em cada parafuso quando a porca é desatarraxada, aliviando, assim, a força de aperto.
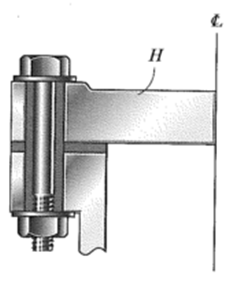
0 (zero) mm
0,025 mm
0,005 mm
1,008 mm
0,008 mm
A junta está presa por dois parafusos. Determine o diâmetro exigido para os parafusos se a tensão de ruptura por cisalhamento para os parafusos for de 350 MPa. Use um fator e segurança por cisalhamento de 2,5.
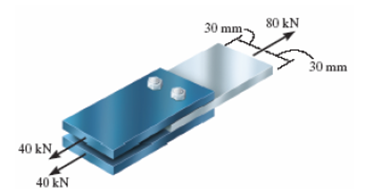
d = 12,10 mm
d = 13,49 mm
d = 15,40 mm
d = 14,39 mm
d = 12,39 mm
O eixo está sujeito à força axial de 30 kN. Se ele passar pelo orifício de 53 mm de diâmetro no apoio fixo A, determine a tensão no mancal que age sobre o colar C. Determine também a tensão de cisalhamento média que age ao longo da superfície interna do colar no ponto onde ele está acoplado ao eixo de 52 mm de diâmetro.
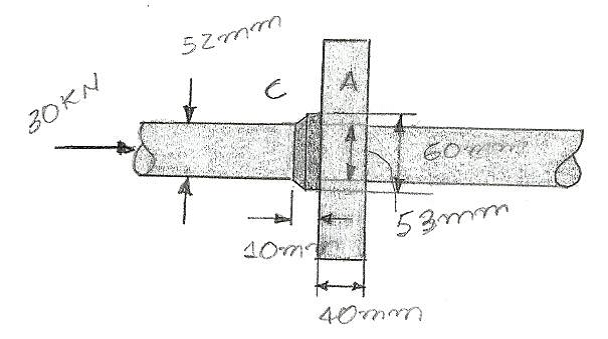
Tmancal = 45,3 MPa e Tméd = 15,4 MPa
Tmancal = 41 MPa e Tméd = 11,4 MPa
Tmancal = 48,3 MPa e Tméd = 18,4 MPa
Tmancal = 47 MPa e Tméd = 17 MPa
Tmancal = 44,3 MPa e Tméd = 14,4 MPa
Determine a tensão de cisalhamento máxima conforme figura.
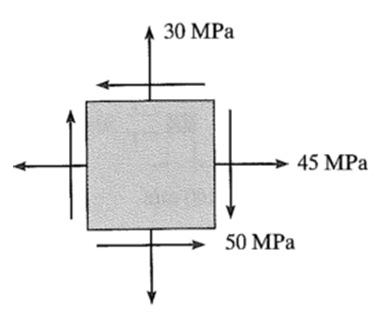
tmáx = 13.06 MPa
tmáx = 55.06 MPa
tmáx = 56.50 MPa
tmáx = 50.56 MPa
tmáx = 88.06 MPa
Determine a tensão normal máxima aplicada no elemento de seção transversal quadrada de lado de 20 cm, apresentado a seguir, solicitado no carregamento de uma viga bi-apoiada com um 1,95 m de comprimento e carregamento distribuído de 1,0 kn/m, conforme apresentado na estrutura abaixo:
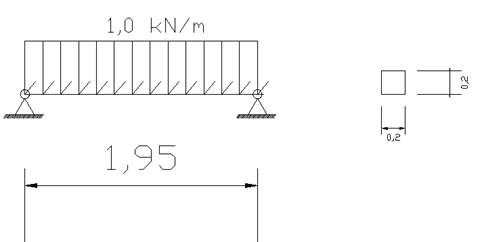
266,50 KPa
156,50 KPa
356,48 KPa
56,50 KPa
146,50 KPa
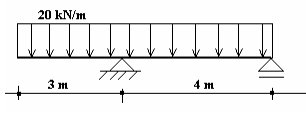
Projetar uma peça com seção retangular com altura igual ao dobro da base para servir como viga conforme a figura abaixo. A viga será construída com material dúctil que apresenta tensão de escoamento de 400 MPa. Despreze o esforço cortante e adote segurança 2,5.
122,98 N.m
243,25 N.m
135,85 N.m
150,34 N.m
170,35 N.m
Uma viga simples AB com um balanço BC suporta um carregamento concentrado P na extremidade do balanço (conforme figura). A extensão principal da viga tem comprimento L e o balanço tem comprimento L/2. Determine a deflexão δC na extremidade do balanço. Use a equação diferencial de terceira ordem da curva de deflexão( a equação da força de cisalhamento). A viga tem rigidez de flexão EI constante.


δc = PL³/8EI
δc = PL³/30EI
δc = PL³/24EI
δc = PL²/3EI
δc = PL³/3EI
O eixo de cobre está sujeito às cargas axiais mostradas na figura. Determine o deslocamento da extremidade A em relação à extremidade D se os diâmetros de cada segmento forem dAB = 20 mm, dBC = 25 mm e dCD = 12 mm. Ecobre = 126 GPa.

+ 23,843 mm
+ 10,254 mm
+ 3,8483 mm
– 3,8483 mm
– 1,2543 mm
Qual o valor da deformação especifica normal de uma barra de comprimento inicial 1,75m, que após a aplicação de uma força passa a medir 1,762 m?
0,000506
0,000476
0,00686
0,000214
0,00706
O cabeçote H está acoplado ao cilindro de um compressor por seis parafusos de aço. Se a força de aperto de cada parafuso for 4 kN, determine a deformação normal nos parafusos. Cada um deles tem 5 mm de diâmetro. Se σe=280 Mpa e Eaço=200 GPa, qual é a deformação em cada parafuso quando a porca é desatarraxada, aliviando, assim, a força de aperto.

0 (zero) mm
0,025 mm
0,005 mm
1,008 mm
0,008 mm
A junta está presa por dois parafusos. Determine o diâmetro exigido para os parafusos se a tensão de ruptura por cisalhamento para os parafusos for de 350 MPa. Use um fator e segurança por cisalhamento de 2,5.

d = 12,10 mm
d = 13,49 mm
d = 15,40 mm
d = 14,39 mm
d = 12,39 mm
O eixo está sujeito à força axial de 30 kN. Se ele passar pelo orifício de 53 mm de diâmetro no apoio fixo A, determine a tensão no mancal que age sobre o colar C. Determine também a tensão de cisalhamento média que age ao longo da superfície interna do colar no ponto onde ele está acoplado ao eixo de 52 mm de diâmetro.

Tmancal = 45,3 MPa e Tméd = 15,4 MPa
Tmancal = 41 MPa e Tméd = 11,4 MPa
Tmancal = 48,3 MPa e Tméd = 18,4 MPa
Tmancal = 47 MPa e Tméd = 17 MPa
Tmancal = 44,3 MPa e Tméd = 14,4 MPa
Determine a tensão de cisalhamento máxima conforme figura.

tmáx = 13.06 MPa
tmáx = 55.06 MPa
tmáx = 56.50 MPa
tmáx = 50.56 MPa
tmáx = 88.06 MPa
Determine a tensão normal máxima aplicada no elemento de seção transversal quadrada de lado de 20 cm, apresentado a seguir, solicitado no carregamento de uma viga bi-apoiada com um 1,95 m de comprimento e carregamento distribuído de 1,0 kn/m, conforme apresentado na estrutura abaixo:

266,50 KPa
156,50 KPa
356,48 KPa
56,50 KPa
146,50 KPa
Projetar uma peça com seção retangular com altura igual ao dobro da base para servir como viga conforme a figura abaixo. A viga será construída com material dúctil que apresenta tensão de escoamento de 400 MPa. Despreze o esforço cortante e adote segurança 2,5.



δc = PL³/8EI
δc = PL³/30EI
δc = PL³/24EI
δc = PL²/3EI
δc = PL³/3EI
O eixo de cobre está sujeito às cargas axiais mostradas na figura. Determine o deslocamento da extremidade A em relação à extremidade D se os diâmetros de cada segmento forem dAB = 20 mm, dBC = 25 mm e dCD = 12 mm. Ecobre = 126 GPa.

+ 23,843 mm
+ 10,254 mm
+ 3,8483 mm
– 3,8483 mm
– 1,2543 mm
Qual o valor da deformação especifica normal de uma barra de comprimento inicial 1,75m, que após a aplicação de uma força passa a medir 1,762 m?
0,000506
0,000476
0,00686
0,000214
0,00706
O cabeçote H está acoplado ao cilindro de um compressor por seis parafusos de aço. Se a força de aperto de cada parafuso for 4 kN, determine a deformação normal nos parafusos. Cada um deles tem 5 mm de diâmetro. Se σe=280 Mpa e Eaço=200 GPa, qual é a deformação em cada parafuso quando a porca é desatarraxada, aliviando, assim, a força de aperto.

0 (zero) mm
0,025 mm
0,005 mm
1,008 mm
0,008 mm
A junta está presa por dois parafusos. Determine o diâmetro exigido para os parafusos se a tensão de ruptura por cisalhamento para os parafusos for de 350 MPa. Use um fator e segurança por cisalhamento de 2,5.

d = 12,10 mm
d = 13,49 mm
d = 15,40 mm
d = 14,39 mm
d = 12,39 mm
O eixo está sujeito à força axial de 30 kN. Se ele passar pelo orifício de 53 mm de diâmetro no apoio fixo A, determine a tensão no mancal que age sobre o colar C. Determine também a tensão de cisalhamento média que age ao longo da superfície interna do colar no ponto onde ele está acoplado ao eixo de 52 mm de diâmetro.

Tmancal = 45,3 MPa e Tméd = 15,4 MPa
Tmancal = 41 MPa e Tméd = 11,4 MPa
Tmancal = 48,3 MPa e Tméd = 18,4 MPa
Tmancal = 47 MPa e Tméd = 17 MPa
Tmancal = 44,3 MPa e Tméd = 14,4 MPa
Determine a tensão de cisalhamento máxima conforme figura.

tmáx = 13.06 MPa
tmáx = 55.06 MPa
tmáx = 56.50 MPa
tmáx = 50.56 MPa
tmáx = 88.06 MPa
Determine a tensão normal máxima aplicada no elemento de seção transversal quadrada de lado de 20 cm, apresentado a seguir, solicitado no carregamento de uma viga bi-apoiada com um 1,95 m de comprimento e carregamento distribuído de 1,0 kn/m, conforme apresentado na estrutura abaixo:

266,50 KPa
156,50 KPa
356,48 KPa
56,50 KPa
146,50 KPa
Projetar uma peça com seção retangular com altura igual ao dobro da base para servir como viga conforme a figura abaixo. A viga será construída com material dúctil que apresenta tensão de escoamento de 400 MPa. Despreze o esforço cortante e adote segurança 2,5.


+ 23,843 mm
+ 10,254 mm
+ 3,8483 mm
– 3,8483 mm
– 1,2543 mm
Qual o valor da deformação especifica normal de uma barra de comprimento inicial 1,75m, que após a aplicação de uma força passa a medir 1,762 m?
0,000506
0,000476
0,00686
0,000214
0,00706
O cabeçote H está acoplado ao cilindro de um compressor por seis parafusos de aço. Se a força de aperto de cada parafuso for 4 kN, determine a deformação normal nos parafusos. Cada um deles tem 5 mm de diâmetro. Se σe=280 Mpa e Eaço=200 GPa, qual é a deformação em cada parafuso quando a porca é desatarraxada, aliviando, assim, a força de aperto.

0 (zero) mm
0,025 mm
0,005 mm
1,008 mm
0,008 mm
A junta está presa por dois parafusos. Determine o diâmetro exigido para os parafusos se a tensão de ruptura por cisalhamento para os parafusos for de 350 MPa. Use um fator e segurança por cisalhamento de 2,5.

d = 12,10 mm
d = 13,49 mm
d = 15,40 mm
d = 14,39 mm
d = 12,39 mm
O eixo está sujeito à força axial de 30 kN. Se ele passar pelo orifício de 53 mm de diâmetro no apoio fixo A, determine a tensão no mancal que age sobre o colar C. Determine também a tensão de cisalhamento média que age ao longo da superfície interna do colar no ponto onde ele está acoplado ao eixo de 52 mm de diâmetro.

Tmancal = 45,3 MPa e Tméd = 15,4 MPa
Tmancal = 41 MPa e Tméd = 11,4 MPa
Tmancal = 48,3 MPa e Tméd = 18,4 MPa
Tmancal = 47 MPa e Tméd = 17 MPa
Tmancal = 44,3 MPa e Tméd = 14,4 MPa
Determine a tensão de cisalhamento máxima conforme figura.

tmáx = 13.06 MPa
tmáx = 55.06 MPa
tmáx = 56.50 MPa
tmáx = 50.56 MPa
tmáx = 88.06 MPa
Determine a tensão normal máxima aplicada no elemento de seção transversal quadrada de lado de 20 cm, apresentado a seguir, solicitado no carregamento de uma viga bi-apoiada com um 1,95 m de comprimento e carregamento distribuído de 1,0 kn/m, conforme apresentado na estrutura abaixo:

266,50 KPa
156,50 KPa
356,48 KPa
56,50 KPa
146,50 KPa
Projetar uma peça com seção retangular com altura igual ao dobro da base para servir como viga conforme a figura abaixo. A viga será construída com material dúctil que apresenta tensão de escoamento de 400 MPa. Despreze o esforço cortante e adote segurança 2,5.

0,000506
0,000476
0,00686
0,000214
0,00706
O cabeçote H está acoplado ao cilindro de um compressor por seis parafusos de aço. Se a força de aperto de cada parafuso for 4 kN, determine a deformação normal nos parafusos. Cada um deles tem 5 mm de diâmetro. Se σe=280 Mpa e Eaço=200 GPa, qual é a deformação em cada parafuso quando a porca é desatarraxada, aliviando, assim, a força de aperto.

0 (zero) mm
0,025 mm
0,005 mm
1,008 mm
0,008 mm
A junta está presa por dois parafusos. Determine o diâmetro exigido para os parafusos se a tensão de ruptura por cisalhamento para os parafusos for de 350 MPa. Use um fator e segurança por cisalhamento de 2,5.

d = 12,10 mm
d = 13,49 mm
d = 15,40 mm
d = 14,39 mm
d = 12,39 mm
O eixo está sujeito à força axial de 30 kN. Se ele passar pelo orifício de 53 mm de diâmetro no apoio fixo A, determine a tensão no mancal que age sobre o colar C. Determine também a tensão de cisalhamento média que age ao longo da superfície interna do colar no ponto onde ele está acoplado ao eixo de 52 mm de diâmetro.

Tmancal = 45,3 MPa e Tméd = 15,4 MPa
Tmancal = 41 MPa e Tméd = 11,4 MPa
Tmancal = 48,3 MPa e Tméd = 18,4 MPa
Tmancal = 47 MPa e Tméd = 17 MPa
Tmancal = 44,3 MPa e Tméd = 14,4 MPa
Determine a tensão de cisalhamento máxima conforme figura.

tmáx = 13.06 MPa
tmáx = 55.06 MPa
tmáx = 56.50 MPa
tmáx = 50.56 MPa
tmáx = 88.06 MPa
Determine a tensão normal máxima aplicada no elemento de seção transversal quadrada de lado de 20 cm, apresentado a seguir, solicitado no carregamento de uma viga bi-apoiada com um 1,95 m de comprimento e carregamento distribuído de 1,0 kn/m, conforme apresentado na estrutura abaixo:

266,50 KPa
156,50 KPa
356,48 KPa
56,50 KPa
146,50 KPa
Projetar uma peça com seção retangular com altura igual ao dobro da base para servir como viga conforme a figura abaixo. A viga será construída com material dúctil que apresenta tensão de escoamento de 400 MPa. Despreze o esforço cortante e adote segurança 2,5.


0 (zero) mm
0,025 mm
0,005 mm
1,008 mm
0,008 mm
A junta está presa por dois parafusos. Determine o diâmetro exigido para os parafusos se a tensão de ruptura por cisalhamento para os parafusos for de 350 MPa. Use um fator e segurança por cisalhamento de 2,5.

d = 12,10 mm
d = 13,49 mm
d = 15,40 mm
d = 14,39 mm
d = 12,39 mm
O eixo está sujeito à força axial de 30 kN. Se ele passar pelo orifício de 53 mm de diâmetro no apoio fixo A, determine a tensão no mancal que age sobre o colar C. Determine também a tensão de cisalhamento média que age ao longo da superfície interna do colar no ponto onde ele está acoplado ao eixo de 52 mm de diâmetro.

Tmancal = 45,3 MPa e Tméd = 15,4 MPa
Tmancal = 41 MPa e Tméd = 11,4 MPa
Tmancal = 48,3 MPa e Tméd = 18,4 MPa
Tmancal = 47 MPa e Tméd = 17 MPa
Tmancal = 44,3 MPa e Tméd = 14,4 MPa
Determine a tensão de cisalhamento máxima conforme figura.

tmáx = 13.06 MPa
tmáx = 55.06 MPa
tmáx = 56.50 MPa
tmáx = 50.56 MPa
tmáx = 88.06 MPa
Determine a tensão normal máxima aplicada no elemento de seção transversal quadrada de lado de 20 cm, apresentado a seguir, solicitado no carregamento de uma viga bi-apoiada com um 1,95 m de comprimento e carregamento distribuído de 1,0 kn/m, conforme apresentado na estrutura abaixo:

266,50 KPa
156,50 KPa
356,48 KPa
56,50 KPa
146,50 KPa
Projetar uma peça com seção retangular com altura igual ao dobro da base para servir como viga conforme a figura abaixo. A viga será construída com material dúctil que apresenta tensão de escoamento de 400 MPa. Despreze o esforço cortante e adote segurança 2,5.


d = 12,10 mm
d = 13,49 mm
d = 15,40 mm
d = 14,39 mm
d = 12,39 mm
O eixo está sujeito à força axial de 30 kN. Se ele passar pelo orifício de 53 mm de diâmetro no apoio fixo A, determine a tensão no mancal que age sobre o colar C. Determine também a tensão de cisalhamento média que age ao longo da superfície interna do colar no ponto onde ele está acoplado ao eixo de 52 mm de diâmetro.

Tmancal = 45,3 MPa e Tméd = 15,4 MPa
Tmancal = 41 MPa e Tméd = 11,4 MPa
Tmancal = 48,3 MPa e Tméd = 18,4 MPa
Tmancal = 47 MPa e Tméd = 17 MPa
Tmancal = 44,3 MPa e Tméd = 14,4 MPa
Determine a tensão de cisalhamento máxima conforme figura.

tmáx = 13.06 MPa
tmáx = 55.06 MPa
tmáx = 56.50 MPa
tmáx = 50.56 MPa
tmáx = 88.06 MPa
Determine a tensão normal máxima aplicada no elemento de seção transversal quadrada de lado de 20 cm, apresentado a seguir, solicitado no carregamento de uma viga bi-apoiada com um 1,95 m de comprimento e carregamento distribuído de 1,0 kn/m, conforme apresentado na estrutura abaixo:

266,50 KPa
156,50 KPa
356,48 KPa
56,50 KPa
146,50 KPa
Projetar uma peça com seção retangular com altura igual ao dobro da base para servir como viga conforme a figura abaixo. A viga será construída com material dúctil que apresenta tensão de escoamento de 400 MPa. Despreze o esforço cortante e adote segurança 2,5.


Tmancal = 45,3 MPa e Tméd = 15,4 MPa
Tmancal = 41 MPa e Tméd = 11,4 MPa
Tmancal = 48,3 MPa e Tméd = 18,4 MPa
Tmancal = 47 MPa e Tméd = 17 MPa
Tmancal = 44,3 MPa e Tméd = 14,4 MPa
Determine a tensão de cisalhamento máxima conforme figura.

tmáx = 13.06 MPa
tmáx = 55.06 MPa
tmáx = 56.50 MPa
tmáx = 50.56 MPa
tmáx = 88.06 MPa
Determine a tensão normal máxima aplicada no elemento de seção transversal quadrada de lado de 20 cm, apresentado a seguir, solicitado no carregamento de uma viga bi-apoiada com um 1,95 m de comprimento e carregamento distribuído de 1,0 kn/m, conforme apresentado na estrutura abaixo:

266,50 KPa
156,50 KPa
356,48 KPa
56,50 KPa
146,50 KPa
Projetar uma peça com seção retangular com altura igual ao dobro da base para servir como viga conforme a figura abaixo. A viga será construída com material dúctil que apresenta tensão de escoamento de 400 MPa. Despreze o esforço cortante e adote segurança 2,5.


tmáx = 13.06 MPa
tmáx = 55.06 MPa
tmáx = 56.50 MPa
tmáx = 50.56 MPa
tmáx = 88.06 MPa
Determine a tensão normal máxima aplicada no elemento de seção transversal quadrada de lado de 20 cm, apresentado a seguir, solicitado no carregamento de uma viga bi-apoiada com um 1,95 m de comprimento e carregamento distribuído de 1,0 kn/m, conforme apresentado na estrutura abaixo:

266,50 KPa
156,50 KPa
356,48 KPa
56,50 KPa
146,50 KPa
Projetar uma peça com seção retangular com altura igual ao dobro da base para servir como viga conforme a figura abaixo. A viga será construída com material dúctil que apresenta tensão de escoamento de 400 MPa. Despreze o esforço cortante e adote segurança 2,5.


266,50 KPa
156,50 KPa
356,48 KPa
56,50 KPa
146,50 KPa
Projetar uma peça com seção retangular com altura igual ao dobro da base para servir como viga conforme a figura abaixo. A viga será construída com material dúctil que apresenta tensão de escoamento de 400 MPa. Despreze o esforço cortante e adote segurança 2,5.

